ETS_LOS_Discussion

Line of Sight (LOS)

LOS Discussion

Line of Sight is a direct imaginary line between two points (for example a line from the center of the eye to the center of the object viewed) uninterrupted by physical matter other than the atmosphere.

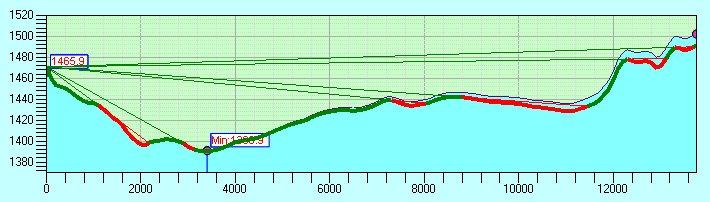
So the problem of defining LOS between 2 points can be stated simply:

If the line between the Observer and the Target intersects the surface (buildings and other opaque objects included in the term surface here) the Target is non visible from the Observer. This can be illustrated with the following image:

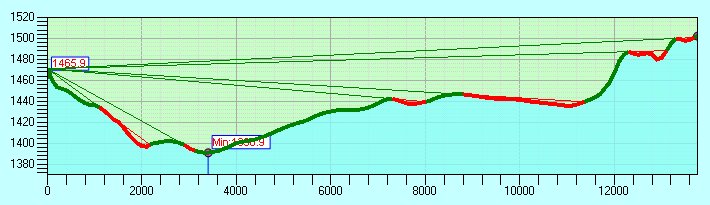
The green parts of the surface will be visible and the red ones non-visible from the Observer.

Earth Curvature

There are however several other factors to consider. The above image will be correct if the Earth is flat and there is no atmosphere. We know however that the Earth is not flat and have to take into account the curvature in our calculations.

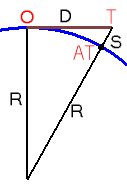		Lets assume an Observer (O) located at sea level that is looking towards a Target (AT) located also at sea level. For the calculations we will assume that the Earth is a sphere. Lets get the radius (R) of the Earth at the Observer and Target points. The radius at the Target will intersect the tangent at the Observer in point T. Lets indicate the sink of the Target due to the curvature of the Earth with S. Using Pythagorean Theorem we can easily obtain the value of the sink (R+S)²= R²+D² R² + 2RS + S² = R^{2 +}D² This can be solved for S as a quadratic equation: S² + 2RS - D2 = 0 (We know R and D) but to simplify the formula, we'll take a different approach S(2R+S) = D² S = D²/(2R+S) Since the radius of the earth R = 6,370,000 meters is significantly (hundreds times) larger than the sink (S) we can accept that 2R+S = 2R (this will give 1 millimeter difference compared to the exact results if calculated for D = 50,000). Therefore our formula for the sink becomes: S = D²/2R From the table on the left we can see that the sink of the target significantly increases with the increase of the distance to the target. Since some obstacles that are between the observer and the target will sink less than the target itself, in many cases we'll have a target that to become invisible
Distance (Meters)	Sink (Meters)
1,000	0.08
5,000	1.96
10,000	7.85
30,000	70.65
50,000	196.23

The image above illustrates how the target sinks (compared with the profile of the surface) with the increase of the distance to the Observer.

Taking into account the refraction of the light

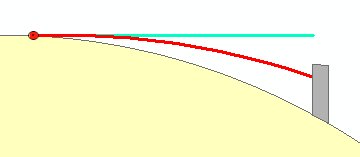As a general atmospheric condition the density of the air decreases as height increases. As a result of this the light tends to bend as it travels long distances through air. This causes distant objects near the horizon to appear higher than they actually are. This negates to some extent the sinking caused by the curvature of the Earth. The refraction coefficient might differ for different atmospheric conditions coefficient of 0.13 can be used for achieving reliable results: R = KD²/2R

K is the refraction coefficient

Line of sight for radio propagation.

There are many factors influencing the trajectory of the radio waves - atmospheric pressure, temperature, etc., but in general it tends to bend toward the Earth and returns to the surface behind the horizon. In practice an Effective Earth Radius Ra = KR is used to take into account the refraction of the radio waves.

For typical atmospheric conditions the correction factor (K) is 4/3.

In other words the distance from the transmitting antenna to where the ray returns to the surface is equivalent to the optical horizon, had the Earth's radius been 4/3 of its actual value.